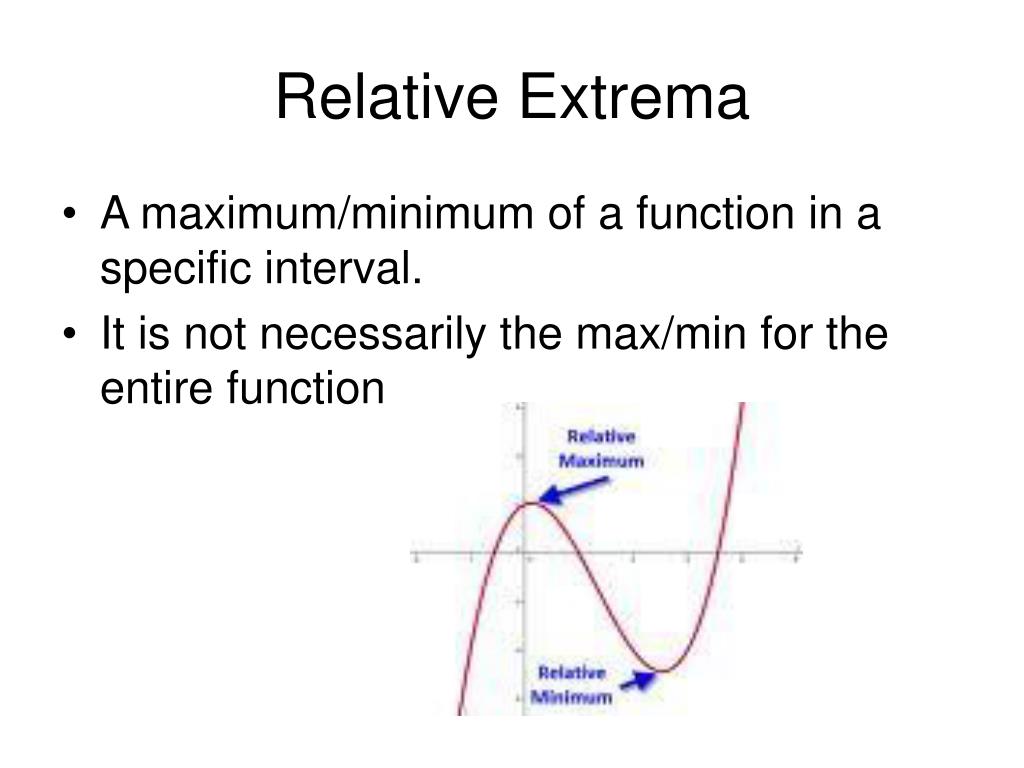
A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. Therefore, when the derivative is zero, the tangent line is horizontal. To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation. Horizontal tangent lines are important in calculus because they indicate local maximum or minimum points in the original function. The derivative of a function has many applications to problems in calculus.
It may be used in curve sketching; solving maximum and minimum problems; solving distance; velocity, and acceleration problems; solving related rate problems; and approximating function values. The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. Because the slopes of perpendicular lines are negative reciprocals of one another, the slope of the normal line to the graph of f is −1/ f′. An online tangent line calculator will help you to determine the tangent line to the implicit, parametric, polar, and explicit at a particular point. Apart from this, the equation of tangent line calculator can find the horizontal and vertical tangent lines as well.
So, keep reading to understand how to find tangent line and slope of a tangent line with the help of tangent line equation. Give an example of a function that has two different horizontal tangent lines. Consider the function Generate the graph of using your calculator. Approximate the slope of the tangent line to the graph at the point Use the following set of x values to generate the sequence of secant line slopes. In general, the shorter the time interval over which we calculate the average velocity, the better the average velocity will approximate the instantaneous velocity.
The average velocity over a time interval is \( \dfrac \), which is the slope of the secant line through two points on the graph of height versus time. The instantaneous velocity at a particular time and height is the slope of the tangent line to the graph at the point given by that time and height. The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. To better understand the relationship between average velocity and instantaneous velocity, see . In this figure, the slope of the tangent line is the instantaneous velocity of the object at time whose position at time is given by the function .
The slope of the secant line is the average velocity of the object over the time interval . The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus.
The slope of the tangent line to a curve measures the instantaneous rate of change of a curve. We can calculate it by finding the limit of the difference quotient or the difference quotient with increment . Use this handy tangent line calculator to find the tangent line to the several curves at the given point with a complete solution. Therefore, students and teachers can perform all these calculations manually.
However, this is a difficult and time-consuming task. By using an online tangent line equation calculator you can determine tangent lines seamlessly at specific points numerous times. Since the derivative is zero or undefined at both local maximum and local minimum points, we need a way to determine which, if either, actually occurs.
So we want to find the tangent line to this curve that's parallel to the line, expose y equals zero. So we'll first need to differentiate using the power rules. Now we know that parallel lines have the same slope. So we want to find out what the slope of this line is, which we can do by rearranging why goes negative X. Which tells us that the slope is negative one. We know that F prime of some number would give us the slope.
So we want to set or derivative equal to negative one to find what X value would produce that slope of the tangent line. So at the x value of two, The Tangent Line would have a slope of -1. And we want to find with the Y value on the original curve.
So we can write an equation of the tangent line, wine minus. Why is the one equals sometimes X- Except one. And we can rearrange us in the point slope form if we'd like by distributing to get the equation of the tangent line, Y equals negative X plus one. In we see that, as the values of approach , the slopes of the secant lines provide better estimates of the rate of change of the function at . Furthermore, the secant lines themselves approach the tangent line to the function at , which represents the limit of the secant lines. Similarly, shows that as the values of get closer to 0, the secant lines also approach the tangent line.
The slope of the tangent line at is the rate of change of the function at , as shown in . A stationary point of a function $f$ is a point where the derivative of $f$ is equal to 0. These points are called "stationary" because at these points the function is neither increasing nor decreasing.
Graphically, this corresponds to points on the graph of $f$ where the tangent to the curve is a horizontal line. As we saw on the previous page, if a local maximum or minimum occurs at a point then the derivative is zero . It is not, however, true that when the derivative is zero we necessarily have a local maximum or minimum. With a maximum we saw that the function changed from increasing to decreasing at that point. With a minimum it changed from decreasing to increasing.
If the function has zero slope at a point, but is either increasing on either side of the point or decreasing on either side of the point we call that a point of inflection. The derivative can be approximated by looking at an average rate of change, or the slope of a secant line, over a very tiny interval. The tinier the interval, the closer this is to the true instantaneous rate of change, slope of the tangent line, or slope of the curve. The tangent at A is the limit when point B approximates or tends to A. A horizontal tangent line is parallel to the x-axis and shows where a function has a slope of zero. You can find these lines either by looking at a graph or by setting an equation to zero to find maximums and minimums.
Just as we have used two different expressions to define the slope of a secant line, we use two different forms to define the slope of the tangent line. In this text we use both forms of the definition. As before, the choice of definition will depend on the setting.
Now that we have formally defined a tangent line to a function at a point, we can use this definition to find equations of tangent lines. Unlike a straight line, a curve's slope constantly changes as you move along the graph. To find the equation for the tangent, you'll need to know how to take the derivative of the original equation. Draw a point on the curve and draw a tangent to that point.
Drag the tangents to the points where the graphs reach a maximum or minimum value. A formula for the derivative function is very powerful, but as you can see, calculating the derivative using the limit definition is very time consuming. In the next section, we will identify some patterns that will allow us to start building a set of rules for finding derivatives without needing the limit definition. The tangent line problem and the instantaneous velocity problem are the same problem. This idea is the key to defining the slope of a curve.
As we have seen throughout this section, the slope of a tangent line to a function and instantaneous velocity are related concepts. Each is calculated by computing a derivative and each measures the instantaneous rate of change of a function, or the rate of change of a function at any point along the function. Therefore with this tangent line calculator, you will be able to calculate the slope of tangent line.
However, an online Point Slope Form Calculator will find the equation of a line by using two coordinate points and the slope of the line. If $(x,f)$ is a point where $f$ reaches a local maximum or minimum, and if the derivative of $f$ exists at $x$, then the graph has a tangent line and the tangent line must be horizontal. This is important enough to state as a theorem, though we will not prove it. Differentiate the equation of the circle and plug in the values of x,y in the derivative. Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point.
This question is significantly different from the previous two questions about average velocity. Here we want the instantaneous velocity, the velocity at an instant in time. Unfortunately the tomato is not equipped with a speedometer so we will have to give an approximate answer.
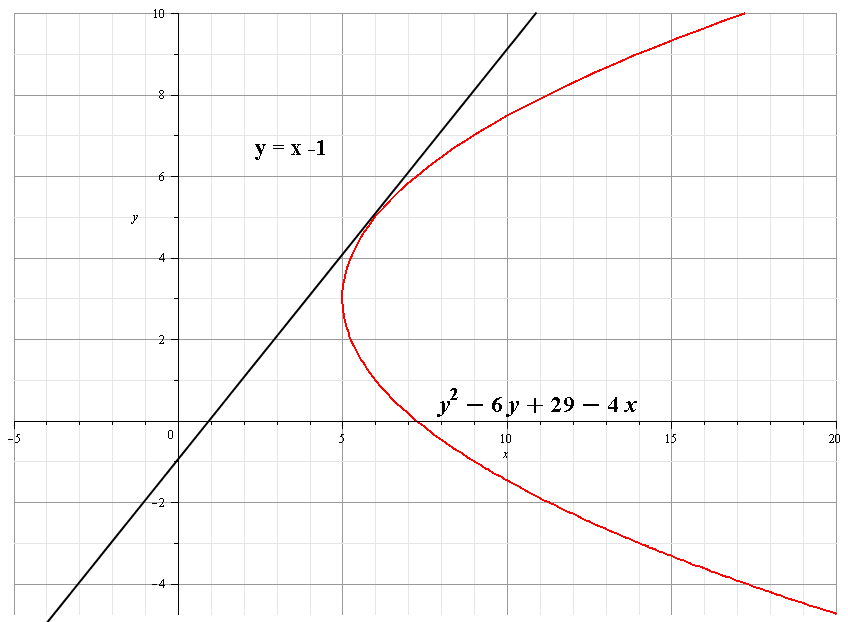
Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents. To determine the equation of a tangent, we need to know the slope of the line as well as the point where it touches the curve. If we take the first-order derivative of the given function and evaluate it at the point of intersection, we can find the slope of a tangent.
Suppose we know the function of the curve, f, that the tangent touches and the x coordinate, x1, of the point of intersection. Then we can follow the steps given below to find the equation of the tangent. Tangent Line Calculator is an online tool that helps to find the equation of the tangent line to a given curve when we know the x coordinate of the point of intersection. The point-slope form of a line can be used to find the equation of a tangent. To use the tangent line calculator, enter the values in the given input boxes. Once you have the slope of the tangent line, which will be a function of x, you can find the exact slope at specific points along the graph.
Since the tangent line touches the circle at just one point, we will never be able to calculate its slope directly, using two "known" points on the line. What we need is a way to capture what happens to the slopes of the secant lines as they get "closer and closer" to the tangent line. The slope of the secant line is the average velocity over the interval . The slope of the tangent line is the instantaneous velocity. The spreadsheet will automatically change A1 to A2, giving you the next approximation.
Continue pasting this into A4, A5, and so on. Each time we paste the formula, we are finding the successive approximations, and each one is getting closer to the root. The second derivative test is used to determine whether a stationary point is a local maximum or minimum. A stationary point $x$ is classified based on whether the second derivative is positive, negative, or zero. In addition to finding the area under a parametric curve, we sometimes need to find the arc length of a parametric curve. In the case of a line segment, arc length is the same as the distance between the endpoints.
If a particle travels from point A to point B along a curve, then the distance that particle travels is the arc length. To develop a formula for arc length, we start with an approximation by line segments as shown in the following graph. These points correspond to the sides, top, and bottom of the circle that is represented by the parametric equations (Figure 1.19). On the left and right edges of the circle, the derivative is undefined, and on the top and bottom, the derivative equals zero.
Find The Points On The Graph Of F Where The Tangent Line Is Horizontal This result is the equation of the tangent line to the given function at the given point. When we have a function that isn't defined explicitly for ??? To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope.
Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. For each possible extreme point, plug the x-coordinate a into f''.
If f'' is positive, there is a local minimum at a. If f'' is negative, there is a local maximum. If f'' is 0, there is an inflection point, not an extreme point. We will have methods for computing exact values of derivatives from formulas soon. If the function is given to you as a table or graph, you will still need to approximate this way.
One crude approximation of the instantaneous velocity after 1 second is simply the average velocity during the entire fall, -40 ft/s . But the tomato fell slowly at the beginning and rapidly near the end so the "-40 ft/s" estimate may or may not be a good answer. Newton's method (also called the Newton–Raphson method) is a way to find x-intercepts of functions. In other words, you want to know where the function crosses the x-axis. The method works well when you can't use other methods to find zeros of functions, usually because you just don't have all the information you need to use easier methods. While Newton's method might look complex, all you're actually doing is finding a tangent line, then another tangent line, and repeat, until you think you're close enough to the actual solution.
As \(\Delta x\) is made smaller , \(7+\Delta x\) gets closer to 7 and the secant line joining \((7,f)\) to \((7+\Delta x,f(7+\Delta x))\) shifts slightly, as shown in Figure 4.1. This is actually quite difficult to see when \(\Delta x\) is small, because of the scale of the graph. The values of \(\Delta x\) used for the figure are \(1\text\) \(5\text\) \(10\) and \(15\text\) not really very small values. The tangent line is the one that is uppermost at the right hand endpoint.
So in this sense, calling it a tangent line seems reasonable. However, the red line also intersects the curve in two places, which suggests the reverse if we adhere to the old geometric definition of a tangent line. Indeed, as we will soon see, the slope of the tangent line at $$ corresponds to the instantaneous velocity this object is traveling at some time $t_0$. Knowing the slopes of tangent lines at various points on the graph of a function can help one better understand the graph of the overall function. Newton's Method is built around tangent lines.









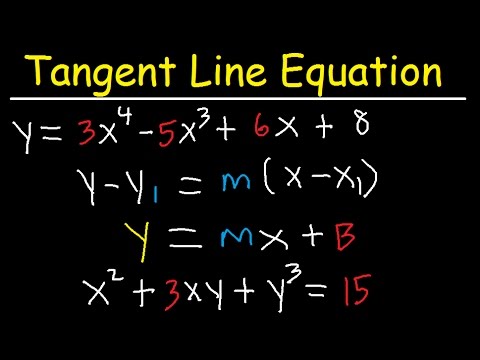













No comments:
Post a Comment
Note: Only a member of this blog may post a comment.